Number Systems ⇒⇒ Exercise 1.2

Question 1(i)

State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.

Solution :

(i)True .

The set of real numbers is comprised of both rational numbers (numbers that can be written as a fraction, like (1/2) and irrational numbers (numbers that cannot be written as a fraction, like ${ \sqrt 5}$ or π).

Therefore, by definition, all irrational numbers are a subset of the real numbers.

Question 1(ii)

State whether the following statements are true or false. Justify your answers.
(ii) Every point on the number line is of the form √m , where m is a Natural number

Solution :

(ii) False .

The number line includes negative numbers (e.g., -2), which cannot be the square root of a natural number. The square root of a natural number is always non-negative.

The square root of a natural number, such as ${ \sqrt 2}$ , corresponds to a point on the number line. However, not all points can be represented this way. For example, ${ \sqrt 1.5}$ is a real number, but 1.5 is not a natural number..

Question 1(iii)

State whether the following statements are true or false. Justify your answers.
(iii) Every real number is an irrational number.

Solution :

(iii) False .

Because , All Rational Numbers and Irrational Numbers together are called Real Number.

Therefore every Irrational number is a Real Number, but every Real Number cannot be an Irrational number.

Question 2

Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

Solution :

No, the square roots of all positive integers are not irrational. The square root of a positive integer is a rational number if the integer is a perfect square.

A perfect square is an integer that results from squaring another integer.

Here is an example: : √49 = 7

If we take a positive integer 49 and its square root is √49 = 7 , which is a rational number.

Because 7 can be written in the form of ${ p \over q} = { 7 \over 1} $.

Where both the numerator and the denominator are integers and the denominator is not zero.

Question 3

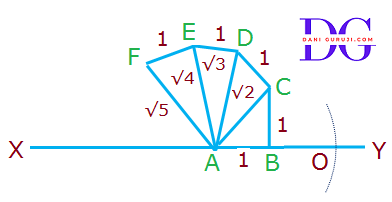
Show how √5 can be represented on the number line.

Solution :

For the square root spiral follow the given steps to show √5 on a number line:

Step: 1 – Draw a number line XY .

Step: 2 – Take AB of length 1 unit

Step: 3 – Draw a perpendicular BC of length 1 unit on point B.

Step: 4 – Now, Join point A and point C forming a line AC.

Step: 5 – This AC will be equal to √2 .This can be easily found using Pythagoras Theorem in right triangle ABC

Step: 6 – Now, Draw a perpendicular CD of length 1 unit at point C and join points A and D.

Step: 7 – Here, AD represents a line of length √3 units

Step: 8 – Now, Draw a perpendicular DE of length 1 unit at point D and join points A and E.

Step: 9 – Here, AE represents a line of length √4 units i.e. equal to 2 unit.

Step: 10 – Now, Draw a perpendicular EF of length 1 unit at point E and join points A and F.

Step: 11 – Here, AF represents a line of length √5 units .

Step: 12 – Taking AF as a radius and A as the center, construct an arc touching the number line.

Step: 13 – The number line gets intersected by the arc at a point O which is at √5 distance from 0, as it is a radius of the circle with center A

Step: 14 – Thus, √5 is represented on the number line as AO

Explanation: how, AF is equal to √5

Now, in △AEF , AE = 2 unit , FE = 1 unit

and ∠AEF = 90º

Thus, according to Pythagoras theorem.

AF² = AE² + EF²

AF² = 2² + 1²

AF² = 4 + 1

AF² = 5

AF = √5